Modeling the Nonlinar Vibrations of Strings

In the previous page we have dealt with linear strings, where the string can be described by methods of linear system theory (transfer function, impulse response, etc.). The ideal string is characterized by the linear wave eqation (see Fig. 1) where y is the displacement of the string at the position x and time t, μ is the mass per unit length, and T is the tension (the force applied for stretching the string). The linear wave equation is obtained by assuming that T is constant, i.e., the elongation coming from the change of the string shape during vibration is negligible compared to the initial elongation (or stretching). In this case the points of the string move only in the y direction (i.e., perpendicular to the string).

However, in real instruments such components are also present in the sound that cannot be modeled by linear theory. For example, the metallic sound of low piano tones cannot be reproduced without modeling the longitudinal motion, leading to the appearance of phantom partials. Phantom partials are components that can be found at certain sum- and difference-frequencies of the transverse components.

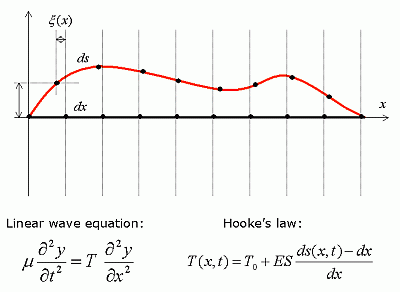
Fig. 1. The geometric nonlinearity

If the string is modeled as a mass-spring network (the points are the masses and the lines between them are the springs in Fig. 1), it is easy to see that at larger amplitudes the points of the string are moving in the  x dircetion, too, as a point that is moved upwards will pull the neighboring ones not only upwards but also towards itself. This excites the longitudinal vibration, which was neglected in the linear model.  As a result, the distance of the points along the string (which now equals ds, and is dx at rest) will vary during vibration. This stretching or compression will lead to a tension variation according to the Hooke's law, which adds up with the tension at rest (T₀) and gives the space- and time dependent tension (T(x,t)). Accordingly, the longitudinal vibration infulences the transverse one through the tension variation. If we wish to model the phenomenon precisely, both the transverse and longitudinal vibrations have to be modeled, toghether with their mutual (and nonlinear) coupling. Note that this nonlinearity comes from the geometry of the problem, and not from the nonlinearity of the string material (as the Hooke's law was applied), hence, it is often called geometric nonlinearity.

Computation of the mutual coupling of the two polarizations is a complicated task, therefore often some simplifications are made. As an example, it is usual to assume that the tension T does not depend on space x, but it varies with time t. This can be used for modeling pitch glides in loosely stretched strings, but it cannot describe the generation of longitudinal vibration and phantom partials, which we are aimed at. A better approximation for our purposes is when T depens both on space and time, but we only model the coupling from the transverse to the longitudinal polarization. In other words, in this model the transverse vibration is not affected by the longitudinal one. This is illustrated in Fig. 2, where it can be seen that the response can be computed in a feedforward way (step by step) as there is no feedback between the model blocks. The transverse vibration can be computed by a linear string model (e.g. one of the methods described for linear string modeling) as a function of the excitation (plucking, strucking, etc.). The longitudinal vibration can be computed by the same formalism, but now the excitation is coming from the transverse vibration, and not from an external device (plectrum or hammer). This feedforward (feedback-less) structure makes the numerical implementation easier. Moreover, it gives the opportunity of computing the string response in a closed form. The closed form solution is of big help for understanding the phenomenon: it can be used for describing the generatoin of phantom partials, which can be useful for acousticians and instrument builders.

Fig. 2. Computation of the transverse and longitudinal vibrations

Naturally, the numerical modeling of the mutual (bi-directional) coupling of the transverse and longitudinal polarizations is also possible. Real strings vibrate in two perpendicular transverse polarizations (in the directions y and z), which can be also modeled. In the case of bowed strings, a forth polarization might need to be computed, as the bow excites torsional vibration in the string, which is coupled with the other polarizations. The question remains whether the significant increase in computational complexity leads to a similar increase in sound quality.

Related publications:

Balázs Bank and László Sujbert, "Generation of longitudinal vibrations in piano strings: From physics to sound synthesis,'' The Journal of the Acoustical Society of America, vol. 117, no. 4, pp. 2268-2278, Apr. 2005. Homepage	The nonlinear vibration of the string and its significance for the piano. Modeling by finite-difference amd modal based methods.
Balázs Bank, Physics-based Sound Synthesis of String Instruments Including Geometric Nonlinearities, Ph.D. thesis, Budapest Univeristy of Technology and Economics, p. 142, Jun. 2006. Homepage	Chapter 5 is about the theory of geometric nonlinearities, while Chap. 6 is about extending the existing linear string models for longitudinal modeling.

Further related papers can be downloaded from this page.

 Further information: Balázs Bank