The architecture of a distributed signal processing system is depicted in Fig. 1. Besides the structure is flexible enough to represent a wide range of distributed systems, it contains all of the important components required for signal processing.

Fig. 1. Block diagram of the system.

A sensor network is attached to a multiple-input multiple-output (MIMO) physical system, and the individual sensors transmit raw or preprocessed measurement data to a central processing unit over a shared communication network. The central unit aggregates the sensors’ data, and generates control signals which are directly connected to the physical MIMO plant. The system model in Fig. 1 clearly shows that signal sensing and processing are performed in a distributed manner by the sensor network and a central controller.

In order to be able to achieve practical experiences and to test the theoretical results, a test system was also developed. The test application selected for the realization using wireless sensors was active noise control (ANC). The architecture of the test system and an experimental arrangement can be seen in Fig. 2 and Fig. 3, respectively.

The choice of ANC as test application was motivated by the knowledge-base obtained in this field in our laboratory, and it is also reasonable from scientific and practical aspects due to the following facts:

• ANC systems are real MIMO systems, the acoustic cross-coupling is formed inherently.
• The acoustic plant is present everywhere, it is easy to install and reconfigure (changing the transfer functions).
• Sensors and actuators (microphones and loudspeakers) are cheap and easily available.
• Real-time feedback is essential.
• The bandwidth of acoustic signal is a real challenge for a sensor network but not impossible.
• Not safety-critical: instability doesn't result in dangerous situation or the damage of the system.

In the test system 8 bit microcontrollers with 2.4 GHz ZigBee radio were deployed as sensors, and the central controller was realized with a 32 bit floating point DSP. The sampling frequency was set to 1.8 kHz.

Synchronization

In traditional centralized signal processing systems, sampling and signal processing are performed on the same device. However, in distributed systems, where the sampling and the signal processing are performed on different devices, the signal is distorted in a sense, which is to be compensated.
Perhaps the most unpleasant effect caused by the distributed signal sensing is the uncertain amount of delay in the data transmission. Since a constant delay can easily be compensated, system designers generally aim to use deterministic protocols for data transmission in order to ensure constant delay. However, the delay caused by the unsynchronized nodes has also serious effect, since it is not known in advance, so its compensation is not possible. The uncertainty of the delay in the feedback can lead even to the instability of the system.
In order to solve the problem of synchronization we have proposed a PLL-like synchronization mechanism as shown in Fig. 4. This mechanism aligns the sampling instants of the different sensor nodes such that the time difference between them remains almost constant, so it can be taken into account during the system design.
 

Fig. 4. Synchronization mechanism.

The effect of unsynchronized operation on the stability of a system is illustrated in Fig. 5, where a resonator-based ANC system was operated with wireless sensors. It is also shown that the synchronization mechanism presented above holds the delay in the feedback loop constant, so it ensures the stability of the system.

Fig. 5. Measurement example for the illustration of the effect of synchronization on the stability (left column: synchronization is inactive, right column: synchronization is active; top: noise signal after ANC has been turned on, bottom: time delay variation).

It can be seen that the delay T_d can be held on a constant level if the synchronization is switched on permanently (bottom right figure), but if the synchronization is switched off, this delay changes continuously (bottom left figure). In our system the excess delay caused by the unsynchronized operation is bounded by one sampling period interval, since the central controller always processes the most recent sample. The time functions on the top show the error signal (remaining noise) after the ANC system has been turned on. One can see that the ANC system works properly if the synchronization is active (top right time function: the error signal is decreased and remains on a constant level), but if the synchronization is inactive, the excess delay T_d changes continuously and if it reaches a critical value indicated with red shaded area, the system becomes unstable, i.e., the error signal increases. The critical delay can be calculated using the stability condition of resonator-based ANC systems.

Bandwidth Limit

In real-time systems, a hard time limit is specified for the transmission time for all of the data collected by the sensors, so the bandwidth limit of the communication channel can be the bottleneck of the whole system. Taking a realistic example, if a 2.4 GHz ZigBee network with 250 kbps bandwidth is used, and an acoustic signal of a bandwidth of 1-2 kHz should be transmitted in real-time, only 3-4 sensors can be deployed in the network taking also into account the communication overhead.
The bandwidth of a communication link is highly determined by standards, costs and the power consumption, so the bandwidth constraints are often resolved by using the computational capacity of the sensor nodes. Intelligent sensors are able to achieve data reduction by preprocessing the signal. Since sensor nodes often have limited computational resources, only a simple method can be used for data compression. In order to alleviate the limitations posed by the bandwidth constraints of communication channel, two solutions are proposed, both of them are based on the local preprocessing of the signal on the sensor nodes:

• sign-error algorithms,
• distributed resonator-based algorithms.

Sign-error algorithms

The basic block diagram of a system implementing a sign-error algorithm is shown in Fig. 6.

Fig. 6. Block diagram of the sign-error algorithms.

The operation principle is very simple, so it can be implemented on sensors with limited resources. The sensor measures the error signal, and performs a one bit truncation, i.e., it forwards only the signum function of the error signal. Since the sign of the error signal can be represented on one bit (it is positive or negative), it means reasonable signal compression. The advantage of the algorithm is its simplicity, and its disadvantage is that the performance is deteriorated: since only the sign of the error signal is known, the parameters of the control signal are tuned with constant steps. The step size of the algorithm should be set as low as possible in order to achieve low steady-state error, but low step size results in slow convergence, hence a trade-off is required.
The algorithm can be further improved if the sensor measures the absolute mean value of the error signal for periods of length L samples, and transmits this mean value to the central controller. This is a trade-off between the two extrema when the amplitude of the error signal is known in every time instant or it is not known at all.
A measurement result can be seen in Fig. 7, where a periodic noise is suppressed using the resonator-based noise control algorithm. As one can conclude, approximately the same steady-state noise suppression is achieved, but the convergence time of the simple sign error algorithm is higher than that of the other two algorithms. However, the performance (noise suppression and convergence speed) of the improved sing-error algorithm is close to the original algorithm, and its communication bandwidth demand is reduced to the half of the original bandwidth.

Fig. 7. Measurement results for the sign-error algorithms.

Distributed resonator-based algorithms

The block diagram of the distributed resonator-based algorithm can be seen in Fig. 8, and its operation principle is as follows. The sensor nodes measure the disturbance signal, and each node implements locally a Fourier-analyzer (FA). Each node transmits the Fourier-coefficients   to the central controller through a gateway, and the central controller uses these coefficients for the tuning of the control signal.
The synchronization should also be solved in this system as well. On the one hand, the synchronous sampling on the sensors should be solved on the sensor nodes using the PLL-like synchronization method shown in Fig. 4, on the other hand the sensors should periodically update the signal frequency and the reference value of the phase of the complex exponential basis function that are used for the Fourier-decomposition.
The advantage of the algorithm is that the Fourier-coefficients can be transmitted to the central controller less frequently than the signal samples, since the Fourier-coefficients change slower than the signal itself. The disadvantage of the algorithm is that it poses severe requirements on the sensor nodes since the Fourier-decomposition should be performed in real time, which is not a simple task on an 8 bit microcontroller. Furthermore, the number of Fourier-coefficients that can be transmitted is limited for two reasons: the limited computational capacity of the sensor nodes and the bandwidth limit of the communication channel. Theoretically, such a system is able to integrate infinite number of sensors. Practical limitations stem from the slow changes of Fourier coefficients and the computational capacity of the central controller.

Fig. 8. Block diagram of the distributed resonator-based algorithms.

Fig. 9 shows a measurement for comparing the original and the distributed resonator based ANC algorithms. As the measurement shows, the steady-state and the transient performance of the distributed resonator-based algorithm is close to that of the original resonator-based algorithm.
 

Fig. 9. Measurement result for the distributed resonator-based algorithm.

Data loss

Data loss cannot be avoided in real-time communication systems due to the time limit of data transmission and the inherently unreliable physical layer. Data loss can be especially dangerous in closed-loop systems, since if one or more samples of the feedback signals are lost, then the control loop becomes temporarily opened. The first straightforward question which emerges is whether the system remains stable depending on the data loss pattern.
In our model the stability of the closed-loop system can easily be ensured, since the plant itself should be stable if adaptive algorithms like LMS or resonator-based structure is used. However, the quality of the convergence is highly influenced by the data loss pattern. Our aim is to find definite conditions for the convergence of the adaptive algorithm. Convergence means that the state variables of the algorithm tend to their optimal values, where the optimal solution is the limit of the variables without data loss.
In order to model the data loss, a so-called data availability indicator function, Kn, is introduced: K_n = 1 if the sample is processed, and K_n = 0 if the sample is lost at time index n. Furthermore let N denote the number of resonators (i.e., the number of Fourier-coefficients used to represent the signal). Fig. 10 also shows how data loss can be taken into account in the signal path: data loss can be modeled as a controlled switch which is closed if a sample is available, and it is open if the sample is unavailable.

Fig. 10. Modeling the data loss in the resonator-based structure.

Our goal regarding the issue of analyzing the effect of data loss on resonator-based algorithms was to find such conditions which enable us to predict whether the state variables of the resonator-based algorithms converge to their optimal values or not. The conditions can be evaluated using the pattern of data loss and the parameters of the algorithm. Since the theory and nomenclature related to the analysis of data loss is extensive, we don’t give here a comprehensive overview of the topic but highlight the most important results, and interested readers are referenced to the pblications at the bottom of this page.
The practically important case, when the data loss doesn't allow the proper convergence of the algorithm is when samples are missing every time from the same position(s) within the periods of the signal transmitted by the sensors. In other words, this is the case when the data loss pattern K_n is correlated with the signal.
Fortunately, one can find also such conditions under which the convergence can exactly be ensured. One of the practically most important conditions is the following: if the data loss ratio is less than a critical value, then the state variables of the resonator-based adaptive controller converge to their optimal values. Data loss ratio can be defined in several ways, but loosely speaking it is the ratio of the number of processed samples to the total number of samples. Some important extensions and corollaries of this condition are found in (e.g., random data loss described by Bernoulli- or Markov-process doesn't hinder the convergence).
As rule of thumb, the critical value of data loss ratio can be approximated by the reciprocal of the number of resonators. For example, if the disturbing signal contains 5 harmonic components, i.e., there are N = 2*5 + 1 = 9 resonators, and the data loss ratio is less than 1/9 = 11.1%, the convergence of the control algorithm can be strongly suspected even without exactly evaluating the conditions.
In order to illustrate the effect of data loss, two simulation examples are shown in Fig. 11. The sampling frequency is 10 kHz, and a periodic disturbing signal with the frequency of 50 Hz is assumed (hence the number of resonators is: N=10 kHz/50 Hz = 200).
On the left figure, the samples are lost with a periodicity of 50 Hz, i.e., every 200th sample is lost periodically, and on the right figure each 201th sample is lost periodically.
In the first case, the data loss pattern is repeated synchronously with the disturbing signal, so the necessary condition of the convergence is not fulfilled. In this case, the parameters of the algorithm don’t converge to their optimum value, which can be detected by observing that the error signal doesn't converge to zero.
In the second case, the data loss ratio is 1/201 = 0.49% which is less than the critical value given by the reciprocal of the number of resonators: 1/N=0.5%, so the parameters of the algorithm converge to their optimum value, which can be detected by observing that the error signal also converges to zero.

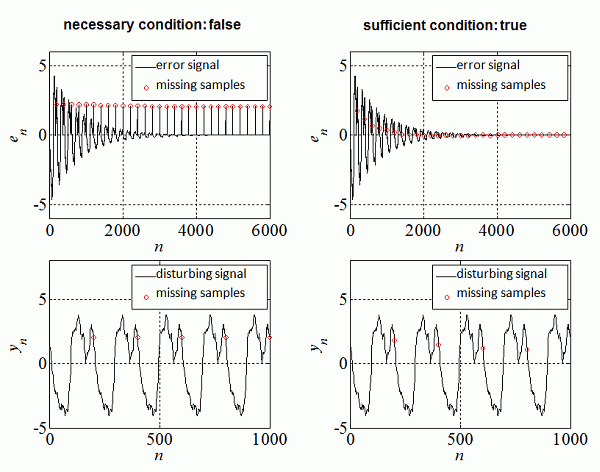
Fig. 11. Simulation example for illustrating the effect of data loss on the resonator-based algorithms.

Related publications

Gy. Orosz, L. Sujbert, G. Péceli „Testbed forWireless Adaptive Signal Processing Systems”, Proc. of the IEEE Instrumentation and Measurement Technology Conf., Warsaw, Poland, pp. 123–128. (1-3 May 2007).	Introduction to the wireless active noise control testbed.
Gy. Orosz, L. Sujbert, G. Péceli „Synchronization and Sampling in Wireless Adaptive Signal Processing Systems”, Periodica Polytechnica-Electrical Engineering, vol. 54, no. 1-2, pp. 59–70 (2010)	The presentation of the synchronization algorithms used in the testbed.
Gy. Orosz, L. Sujbert, G. Péceli „Adaptive Filtering with Bandwidth Constraints in the Feedback Path”, Signal Processing, vol. 92, no. 1, pp. 130–138 (Jan. 2012)	Introduction to the signed-error FxLMS algorithm.
Gy. Orosz, L. Sujbert, G. Péceli „Analysis of Resonator-Based Harmonic Estimation in Case of Data Loss”, IEEE Transactions on Instrumentation and Measurement, vol. 62, no. 2, pp. 510-518., Feb. 2013, doi: 10.1109/TIM.2012.2215071.	The effect of data loss on the resonator-based spectrum estimation.
Orosz György: Rezonátor alapú jelfeldolgozás (Rsonator-based Signal Processing, In Hungarian), PhD dissertation, BME-MIT (2013)	Summary of the results achieved in the field of distributed signal processing systems.
L. Sujbert, "Modellalapú jelfeldolgozás és aktív zajcsökkentés", Dr. Habil. theses (in Hungarian), Budapest University of Technology and Economics, Hungary, p. 47, 2016.	Another summary, further results are included.
L. Sujbert, Gy. Orosz: FFT-based Spectrum Analysis in the Case of Data Loss, IEEE Trans. on Instrumentation and Measurement, vol. 65, no. 5, pp. 968-976, May 2016.	Results about the effect of data loss on the FFT based spectrum estimation.

Further publications on distributed systems can be downloaded from here.

 Further information: György Orosz