Resonator-based Observer

The basic idea is that an effective signal processing algorithm can be established if the structure of the procedure is determined by the structure of the signal generator itself. Hence a signal generator is needed, which can be called conceptual signal model. Therefore the signal processing algorithm will be an observer of the signal generator. In our case the conceptual signal model generates band-limited periodic signals.

Fig. 1. Conceptual signal model

The conceptual signal model is based on the well-known Fourier expansion. In Fig. 1 the generation of the signal can be easily recognized: each channel generates a Fourier component, the sum of which is the output. The multipliers at the channels are the basis functions of the expansion. The multipliers modulate the outputs of the integrators, which have no input. The expression of the basis functions is the following:

where f₁ is the fundamental frequency. The number of the components is N = 2L + 1. The generation of a given periodic signal y_n can be so interpreted, that the integrators, which have no input at the beginning, at time instant n receive at their input the corresponding Fourier coefficients. The outputs of the integrators (which are also he state variables) keep the coefficients. If the inputs of the integrators are excited, a time-variant output signal is generated. An alternative generator can be seen in Fig. 2.

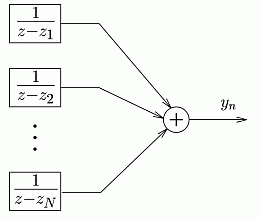
Fig. 2. Conceptual signal model with resonators

The state variables of this model are the weighted complex exponentials, according to the Fourier expansion. The channels of the two models are equivalent, as it can be seen in Fig. 3:

The state variables of this model are the weighted complex exponentials, according to the Fourier expansion. The channels of the two models are equivalent, as it can be seen in Fig. 3:

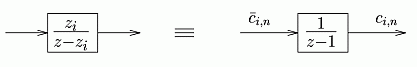
Fig. 3. Equivalence of the two versions of the conceptual signal model

Now an observer has to be designed for the signal model. Since the conceptual signal model has only one output and no excitation, and it is totally observable, therefore a Luenberger-type observer can be designed relatively easily. It can be seen in Fig. 4.

Based on observer theory, a state observer of any characteristic polynomial can be designed. Moreover, as it is meaningful in some cases, the resonator positions can also be arbitrary. However, here only the case of the Fourier expansion is assumed. Furthermore, the most special case is when f₁ = 1/N. In this case the resonators are the Nth roots of the unity in the complex plane, so they have a uniform distribution on the unit circle. The input coefficients required by a dead-beat observer are:

Observer can be designed for that conceptual signal model which can be seen in Fig. 1. In this case instead of the coefficients g_i time-variant multipliers have to be used. The system can be seen in Fig. 5.

The state variables of the observer are the Fourier coefficients. If the system has a finite impulse response, the functions g_i,n are called reciprocal basis functions. If the resonators are distributed uniformly on the unit circle, the coefficients that guarantee finite settling are the following:
 

In this case the structure performs the discrete Fourier transform (DFT), and the state variables are the result of the transform.

The introduction of the resonator based structure shall be completed by the presentation of some transfer functions. The transfer function of one channel is:

The transfer function of the closed loop from the input to the feedback signal is:

which has a very simple form if the system has a finite impulse response and the resonators are distributed uniformly on the unit circle:

which is in accordance with the N step delay of the DFT. The transfer function from the input to the error signal is:

E(z) has zeros at the resonator frequencies, therefore it is a comb filter at the frequencies of the periodic signal model. The "width" of the zeros depends on the loop gain, i.e. the input coefficients: the smaller their absolute value, the narrower the filter. In the case of the DFT (N=9) |E(f)| can be seen in Fig. 6. Here frequency means relative frequency, so e.g., f = 1 belongs to the actual sampling frequency.

Finally, the transfer function of one channel in the closed loop is:

which is in the case of the DFT can be expressed in the well-known form:

where f_i denote the resonator frequency. An example for i= 4, N = 9 can be seen in Fig. 7.

The resonator-based observer structure is successfully applied on those fields where the periodic signal model is adequate, particularly for the calculation of the recursive DFT. It can be used for the implementation of any orthogonal transform (e.g. Walsh-Hadamard transform), as well.

Related Publications:

G. Péceli, "A common structure for recursive discrete transforms", Transactions on Circuits and Systems vol. CAS-33 pp. 1035-36, Oct. 1986.	Introduction of the observer able to perform recursive transforms.
Péceli G., "Valós ideju jelkiértékelés mérési eljárásokban", akadémiai doktori értekezés, DSc thesis (in Hungarian), Hungarian Academy of Sciences, 1988. 211 p.	Overview of the applications of the resonator-based observer.
L. Sujbert, "Periodikus zavarhatások csökkentésének aktív módszerei", Ph.D. thesis (in Hungarian), Budapest University of Technology, Budapest, 1997, 95 p.	The work describes the resonator-based structure in detail.

Further publications related to this topic can be found on this page.

 Futher informatoin: László Sujbert