|
Adaptive Fourier Analysis
The resonator-based observer provides the exact analysis of the
signals which can be described by the supposed signal model. However, if the
fundamental frequency of the input signal differs from that of the supposed one,
the estimation of the components is distorted. This distortion is the well-known
"picket fence" and "leakage" in the case of the DFT. The adaptive Fourier
analyzer (AFA) eliminates these problems. The AFA is such a resonator-based
structure, the resonator poles of which are tuned to coincide with those of the
input signal components. It ensures the perfect decomposition of the input
signal. Fig. 1. shows that version of the observer which is the best to
introduce the AFA algorithm.

Fig. 1. Resonator-based observer
The operation of the channels can be so interpreted, that the
error signal is first mixed to zero frequency by the corresponding
gk,n function, then, after the integration the signal is mixed
back to the original frequency by the ck,n function. If the
observer matches the input signal, the state variables do not change. However,
if there is frequency mismatch, the mixing results in a low-frequency signal.
The state variable in steady state is a rotating complex vector, and the speed
of the rotation corresponds to the actual frequency difference. It can be
utilized for the adaptation of the frequency, according to the following
equation:
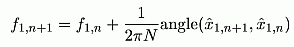
where x1,n with "hat" denotes the state
variable belonging to the fundamental frequency, and "angle" is a function
providing the angle between two complex vectors. The basis functions in the next
time step can be expressed by the new frequency:
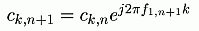
The observer shall use always the adapted basis functions. The
structure performing the DFT has finite settling. However, if the fundamental
frequency changes, the original coefficients gi,k do not
ensure the finite settling. Calculation of new coefficients is disadvantageous,
because of numerical problems and its high computational demand. Fortunately, if
the resonator distribution remains more or less uniform, the system remains
fairly fast. For signals changing in a wide range, it can be ensured by
originating new resonators or dissolving those which are above f = 0.5.
The system shall contain always as many resonators as can be set according to
the band limit. The initialization of the new resonators is the following:
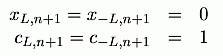
Based on the algorithm described above a family of adaptive
Fourier analyzers has been developed. The original AFA estimates the frequency
of sweeping periodic signals only with constant error, so the signal
reconstruction is also not perfect. Later on analyzers have been developed for
linear, logarithmic and hyperbolic frequency sweeps. The stability of the AFA
algorithm is not obvious, and the analysis is difficult, due to the nonlinear
problem.
Figure 2 shows the operation of the AFA. A signal is connected
at time instant 0 to the input of the system which has a relative frequency of
f = 0.077. The frequency is intentionally not a round number. The signal
is a band limited symmetric triangular signal consisting of 3 nonzero components
as it can be seen in the left top diagram of the figure. Below the magenta curve
shows the estimator of the frequency as function of time. The frequency at the
beginning is around f = 0.025, which the observer has to be set from. The
green curve in the right top corner shows the error signal. It this error signal
converges to zero, the signal reconstruction is perfect, so this signal is
always displayed during research and development works. The diagram in the right
bottom corner shows the estimated amplitude of the harmonic components. It can
be clearly seen that the settling is complete after about 100 samples. Since the
new frequency is about 3 times greater than the original one, structural
adaptivity is needed, i.e. dissolving resonators. This is why the settling is
not exponential as it is usual in linear, time invariant systems.
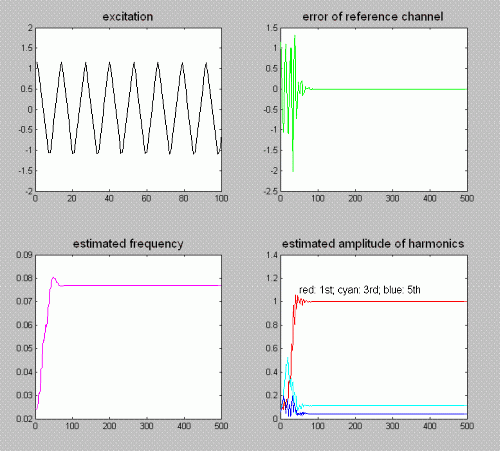
Fig. 2. Operation of the AFA
Another companion page introducing AFA with downloadable Matlab
scripts: http://mit.bme.hu/~sujbert/afa
Related Publications:
|
F. Nagy, "Measurement of signal parameters using nonlinear observers,"
IEEE Transactions on Instrumentation and Measurement, vol.
IM-41,pp. 152-155, Febr. 1992. |
Introduction to the AFA algorithm. |
|
F. Nagy, "An adaptive Fourier analysis algorithm" 5th International
Conference on Signal Processing Applications and Technology, Oct.
18-21, 1994, Dallas, Texas, USA, pp. 414-418. |
Description of an AFA that can follow signals of varying
frequency. |
|
L. Sujbert, G. Simon and A. Várkonyi-Kóczy, "An improved adaptive Fourier analyzer",
Proceedings of the IEEE International Workshop on Intelligent signal
Processing, Sept. 1999, Budapest, Hungary, pp. 182-187. |
Description of an improved AFA that can operate in a wider
frequency range. |
|
L. Sujbert, G. Simon and G. Peceli, "An Observer-Based Adaptive Fourier
Analysis [Tips & Tricks]", IIEEE Signal Processing
Magazine, vol. 37, no. 4, pp. 134-143, July 2020, doi:
10.1109/MSP.2020.2982167. |
Description of the AFA
algorithm. |
Further related publications can be found on this page.
Further information: László Sujbert
|