|
Resonator-based Observer
The basic idea is that an effective signal processing algorithm
can be established if the structure of the procedure is determined by the
structure of the signal generator itself. Hence a signal generator is needed,
which can be called conceptual signal model. Therefore the signal processing
algorithm will be an observer of the signal generator. In our case the
conceptual signal model generates band-limited periodic signals.
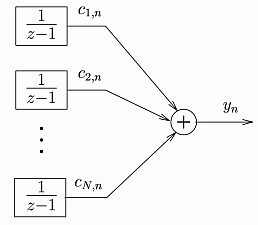
Fig. 1. Conceptual signal model
The conceptual signal model is based on the well-known Fourier
expansion. In Fig. 1 the generation of the signal can be easily recognized: each
channel generates a Fourier component, the sum of which is the output. The
multipliers at the channels are the basis functions of the expansion. The
multipliers modulate the outputs of the integrators, which have no input. The
expression of the basis functions is the following:
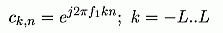
where f1 is the fundamental frequency. The
number of the components is N = 2L + 1. The generation of a given
periodic signal yn can be so interpreted, that the
integrators, which have no input at the beginning, at time instant n receive at
their input the corresponding Fourier coefficients. The outputs of the
integrators (which are also he state variables) keep the coefficients. If the
inputs of the integrators are excited, a time-variant output signal is
generated. An alternative generator can be seen in Fig. 2.
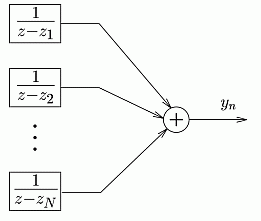
Fig. 2. Conceptual signal model with resonators
The state variables of this model are the weighted complex
exponentials, according to the Fourier expansion. The channels of the two models
are equivalent, as it can be seen in Fig. 3:
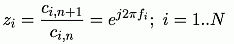
The state variables of this model are the weighted complex
exponentials, according to the Fourier expansion. The channels of the two models
are equivalent, as it can be seen in Fig. 3:
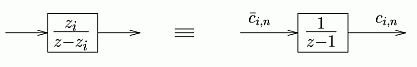
Fig. 3. Equivalence of the two versions of the
conceptual signal model
Now an observer has to be designed for the signal model. Since
the conceptual signal model has only one output and no excitation, and it is
totally observable, therefore a Luenberger-type observer can be designed
relatively easily. It can be seen in Fig. 4.
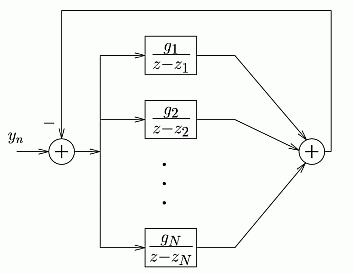
Fig. 4. Observer for periodic signals with resonators
Based on observer theory, a state observer of any
characteristic polynomial can be designed. Moreover, as it is meaningful in some
cases, the resonator positions can also be arbitrary. However, here only the
case of the Fourier expansion is assumed. Furthermore, the most special case is
when f1 = 1/N. In
this case the resonators are the Nth roots of the unity in the complex
plane, so they have a uniform distribution on the unit circle. The input
coefficients required by a dead-beat observer are:
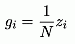
Observer can be designed for that conceptual signal model which
can be seen in Fig. 1. In this case instead of the coefficients gi
time-variant multipliers have to be used. The system can be seen in Fig.
5.
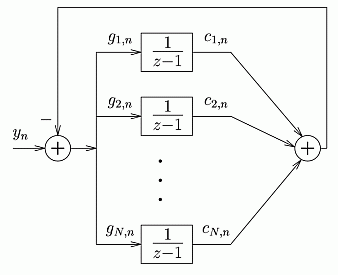
Fig. 5. Observer for periodic signals with integrators
The state variables of the observer are the Fourier
coefficients. If the system has a finite impulse response, the functions
gi,n are called reciprocal basis functions. If the resonators
are distributed uniformly on the unit circle, the coefficients that guarantee
finite settling are the following:
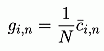
In this case the structure performs the discrete Fourier
transform (DFT), and the state variables are the result of the transform.
The introduction of the resonator based structure shall be
completed by the presentation of some transfer functions. The transfer function
of one channel is:
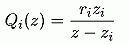
The transfer function of the closed loop from the input to the
feedback signal is:
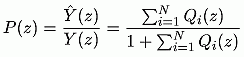
which has a very simple form if the system has a finite impulse
response and the resonators are distributed uniformly on the unit circle:
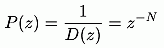
which is in accordance with the N step delay of the DFT.
The transfer function from the input to the error signal is:
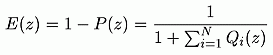
E(z) has zeros at the resonator frequencies, therefore
it is a comb filter at the frequencies of the periodic signal model. The "width"
of the zeros depends on the loop gain, i.e. the input coefficients: the smaller
their absolute value, the narrower the filter. In the case of the DFT
(N=9) |E(f)| can be seen in Fig. 6. Here frequency
means relative frequency, so e.g., f = 1 belongs to the actual sampling
frequency.
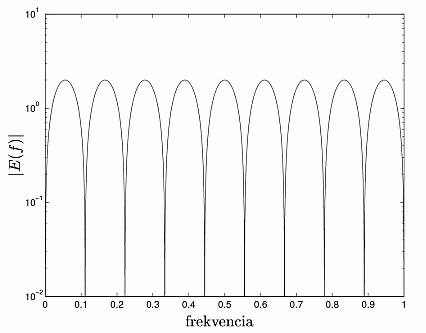
Fig. 6. Magnitude response of the error signal
Finally, the transfer function of one channel in the closed
loop is:
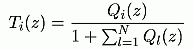
which is in the case of the DFT can be expressed in the
well-known form:
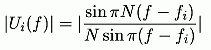
where fi denote the resonator frequency. An
example for i= 4, N = 9 can be seen in Fig. 7.
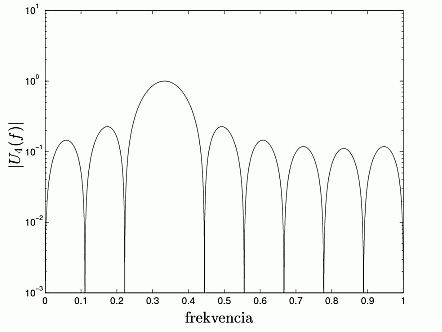
Fig. 7. Magnitude response of one channel of the
observer
The resonator-based observer structure is successfully applied on those
fields where the periodic signal model is adequate, particularly for the
calculation of the recursive DFT. It can be used for the implementation of any
orthogonal transform (e.g. Walsh-Hadamard transform), as well.
Related Publications:
|
G. Péceli, "A common structure for recursive discrete transforms",
Transactions on Circuits and Systems vol. CAS-33 pp. 1035-36, Oct.
1986. |
Introduction of the observer able to perform recursive
transforms. |
|
Péceli G., "Valós ideju jelkiértékelés mérési
eljárásokban", akadémiai doktori értekezés, DSc thesis (in Hungarian),
Hungarian Academy of Sciences, 1988. 211 p. |
Overview of the applications of the resonator-based
observer. |
|
L. Sujbert, "Periodikus zavarhatások csökkentésének
aktív módszerei", Ph.D. thesis (in Hungarian), Budapest
University of Technology, Budapest, 1997, 95 p. |
The work describes the resonator-based structure in
detail. |
Further publications related to this topic can be found on this page.
Futher informatoin: László Sujbert
|